In this post, I will be going through the forward algorithm and the usages of this algorithm in Hidden Markov Models. In the image below we can see the probabilistic graphical model depicting a hidden markov model. The $z_k$ correspond to the unobserved random variables called hidden or latent variables and $x_k$ correspont to the observed ones.

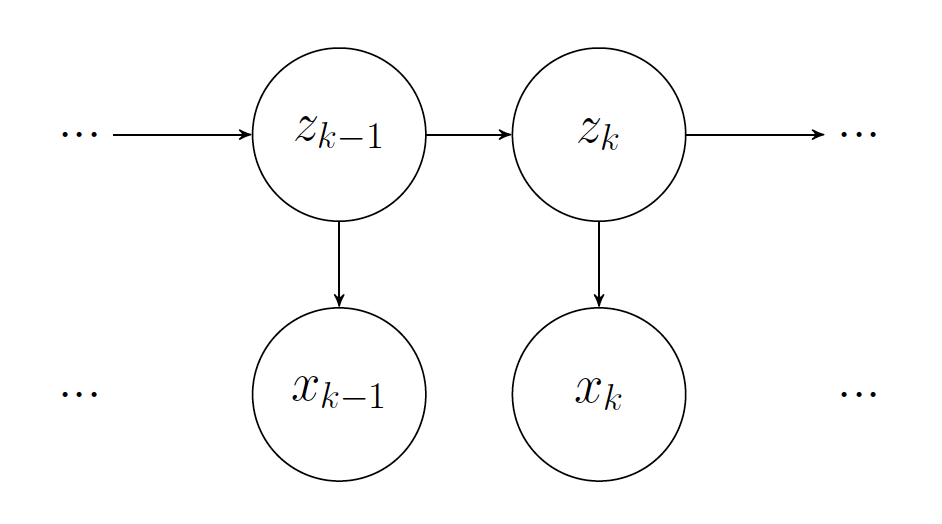
Our goal is to compute: $\small p(z_k,x_{1:k})$ where $\small x_{1:k}=(x_1,…,x_k)$

We assume we know the emission probability distribution $\small p(x_{k}|z_{k})$ and the transition probability distribution $\small p(z_{k}|z_{k-1})$

The forward algorithm uses Dynamic Programming ro decrease computational complexity. So the first thing we need to do is to find a way to state that recursion. What we could do is explicitly add the previous hidden random variable back like so:

We know $\small p(z_{k},x_{1:k})$ is the marginal distribution over the subset $\small (z_{k},x_{1:k})$ and that marginalization is the process of summming the joint distribution over all values of the variable or variables being discarded. So we will make that summation explicit in order to get $\small z_{k-1}$ back:

p(zk,x1:k)=∑zk−1p(zk,zk−1,x1:k)\large p(z_{k},x_{1:k}) =\sum_{z_{k-1}} p(z_{k},z_{k-1},x_{1:k})

Next, we are going to expand this join probability into the following by using the chain rule of probability:

∑zk−1p(zk,Zk−1,x1:k)=∑zk−1p(xk∣zk,zk−1,x1:k−1)p(zk∣zk−1,x1:k−1)p(zk−1,x1:k−1)\large \sum_{z_{k-1}} p(z_{k},Z_{k-1},x_{1:k})=\sum_{z_{k-1}} p(x_{k}|z_{k},z_{k-1},x_{1:k-1})p(z_{k}|z_{k-1},x_{1:k-1})p(z_{k-1},x_{1:k-1})

Then you probably start to see the pattern, where now our computation has become recursive and our joint probability depends now on the joint probability one step back.

One thing about Hidden Markov Models is its Markov property and we can use that to look for conditional independence in our Bayesian Network. So for example, $\small x_{k}$ is independent of $\small z_{k-1}$ and $\small x_{1:k-1}$ given $\small z_{k}$. The same goes for $\small z_{k}$ that is independent of $\small x_{1:k-1}$ given $\small z_{k-1}$

So our equation ends up like this:

p(zk,x1:k)=∑zk−1p(xk∣zk)p(zk∣zk−1)p(zk−1,x1:k−1)\large p(z_{k},x_{1:k}) = \sum_{z_{k-1}} p(x_{k}|z_{k})p(z_{k}|z_{k-1})p(z_{k-1},x_{1:k-1})

So now we can check what we have got so far. The first term $\small p(x_{k}|z_{k})$ is known and the second term $\small p(z_{k}|z_{k-1})$ as well being the first one the emission probability and the second one the transition probability.

Let us rewrite the equation as follows:

αk(zk)=∑zk−1p(xk∣zk)p(zk∣zk−1)αk−1)fork=2,...,n\large \alpha_k(z_k) = \sum_{z_{k-1}} p(x_k|z_k)p(z_k|z_{k-1})\alpha_{k-1})\quad for \quad k=2,...,n

The only thing left is defining $\small \alpha_1 = p(z_1,x_1) = p(z_1)p(x_1|z_1)$ where $\small p(z_1)$ is the initial distribution.

So the computational complexity of this algorithm is $\small O(nm^2)$ being $\small n$ the number of steps and $\small m$ the possible hidden states. We need $\small m$ computations for each $\small z_k$ (the summation) and there are $\small m$ $\small z_k$ and that is for each value of $\small k$ (the steps of the hidden markov model).